Albert Einstein a dit un jour: « L'intérêt composé est le 8e merveille du monde. Celui qui le comprend, le mérite; celui qui ne le fait pas, le paie.
Malgré cette citation impressionnante, l'intérêt composé reste l'un des concepts les plus mal compris. En réalité, quand j'ai demandé sur Twitter, la grande majorité des réponses concernaient des intérêts composés.
Nous n'avons pas de statistiques pour savoir si cela est vrai… mais il se sent comme si c'était vrai.
Mais la réalité est que le pouvoir des intérêts composés ne se limite pas aux mathématiques et à l'argent. Le pouvoir de l'intérêt composé n'est pas dans l'intérêt réel mais dans ce que cela signifie pour vous, les relations et la façon d'amasser de la richesse.
Nous allons d'abord discuter des mathématiques et faire un suivi avec comment cela s'applique à la vie.
Qu'est-ce que l'intérêt composé ?
Si vous ne comprenez pas bien pourquoi les intérêts composés sont si importants, ne vous inquiétez pas. Tu n'es pas seul.
Quand j'ai demandé à Twitter le
un concept financier que la plupart des gens ne comprennent pas, la réponse la plus courante était l'intérêt composé.Intérêts composés est l'intérêt calculé sur votre capital et les intérêts accumulés de toutes les périodes précédentes. L'instrument documentera la fréquence à laquelle il se compose - annuellement, semestriellement (2x par an), trimestriellement, mensuellement, quotidiennement ou en continu. C'est composé parce que le montant s'appuie sur lui-même. C'est puissant car, au fil du temps, un petit montant peut s'accumuler pour en faire un bien plus important si vous ne retirez rien.
L'autre version d'intérêt est connue sous le nom d'intérêt simple. Avec l'intérêt simple, vous ne gagnez des intérêts que sur le capital et non sur les intérêts courus des périodes précédentes. Si vous avez un actif qui génère des intérêts et que ces intérêts sont déposés ou transférés sur un autre compte, il s'agit généralement d'intérêts simples.
La plupart des produits de dépôt, comme un certificat de dépôt, utilisez les intérêts composés.
Formule d'intérêt composé
Pour calculer les revenus d'un actif en fonction de son taux d'intérêt, de sa période et de son temps, utilisez cette équation :
Où:
- FV = Valeur future
- PV = valeur actuelle
- n = périodes de composition par an
- i = taux d'intérêt
- t = temps en années
Formule d'intérêt composé continu
La composition continue est un cas particulier car vous calculez les intérêts sur la base d'un nombre infini de périodes, ce qui implique mathématiquement des limites - vous pouvez le rechercher, mais il ne s'agit que de cette équation :
Où:
- FV = Valeur future
- PV = valeur actuelle
- e 2,7183 (c'est une constante mathématique)
- i = taux d'intérêt
- t = temps en années
C'est une idée si simple mais elle est puissante - alors pourquoi si peu de gens la comprennent-ils ?
Pourquoi les gens n'obtiennent-ils pas des intérêts composés ?
Il existe une citation puissante qui illustre la raison fondamentale pour laquelle certaines personnes ne comprennent pas (et ne profitent pas) des intérêts composés.
Cela a été dit par beaucoup de gens, mais la fois où je l'ai vu, et quand cela a pris résidence dans mon cerveau, c'est lorsque Bill Gates a écrit dans la postface de son livre The Road Ahead :
Nous surestimons toujours le changement qui se produira dans les deux prochaines années et sous-estimons le changement qui se produira dans les dix prochaines. Ne vous laissez pas bercer par l'inaction.
Il faisait référence à la croissance de la technologie et d'Internet.
Il est toujours difficile de voir quelque chose qui n'est pas là. Il est encore plus difficile de voir quelque chose qui sera là dans le futur. C'est pourquoi agents immobiliers mettre en scène une maison avant de la montrer. Même voir les meubles d'autres personnes dans une pièce vide est mieux que de voir une pièce vide parce qu'au moins vous voyez quelque chose.
Si une pièce est difficile à imaginer, pouvez-vous imaginer essayer d'envisager votre vie dans cinq ans? Dix ans? Il y a quelques années, Merrill Edge a publié une application de vieillissement du visage qui a aidé les gens à mieux voir leur avenir. C'était fantaisiste et cela vous montrait juste un visage plus âgé, qui n'était probablement pas à quoi ressemblerait votre visage à l'époque, mais c'est comme mettre en scène une maison. Ton vieux visage valait mieux que de ne pas voir une version de ton futur visage.
C'est pourquoi les gens ont du mal à comprendre le pouvoir des intérêts composés.
Nous sommes terribles à voir l'avenir!
Aidons-vous à visualiser l'intérêt composé
Une partie du problème est que nous ne regardons aussi que des chiffres. Les nombres sont abstraits. Vous n'en avez pas neuf. Vous avez neuf de quelque chose.
À quoi ressemble 1 000 $ lorsque vous lui accordez un taux d'intérêt composé de 5 % pendant quarante ans ?
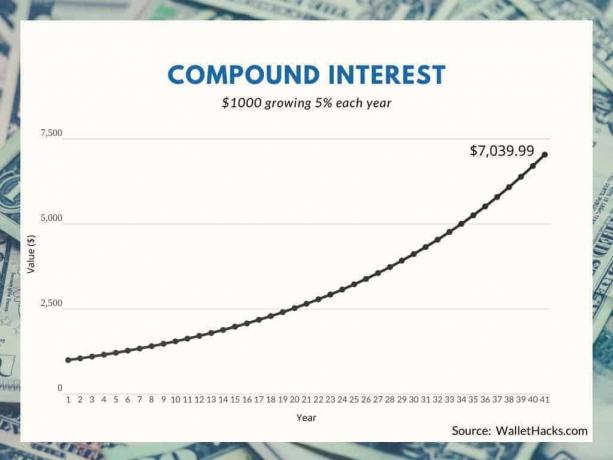
Que se passe-t-il si vous commencez avec 1 000 $ et lui donnez un intérêt composé de 5 % PLUS vous ajoutez une contribution de 1 000 $ chaque année ?

Bien sûr, le deuxième graphique est beaucoup plus gros, vous avez cotisé 41 000 $ sur quarante ans contre seulement 1 000 $ – mais il montre pourquoi les intérêts composés sont si puissants.
Mais un graphique n'est toujours qu'un graphique. C'est juste une ligne avec quelques chiffres. C'est difficile à VOIR.
Comment pouvons-nous mettre cela dans des termes que vous apprécierez ?
Et si vous calculiez combien d'heures vous auriez besoin de travailler pour combler la différence entre ce que vous avez accumulé et ce que vous avez cotisé? Dans le deuxième graphique, vous avez cotisé 41 000 $ mais vous avez amassé un pécule de près de 128 000 $ – une différence de 87 000 $.
Combien d'heures devez-vous travailler pour obtenir 87 000 $? Si vous ne connaissez pas votre taux horaire approximatif mais que vous recevez un salaire, divisez simplement votre salaire annuel par 2 000. C'est 50 semaines de travail, en supposant deux semaines de vacances, et une approximation assez proche.
Si vous gagnez 50 000 $, vous gagnez 25 $ de l'heure. 87 000 $ = 3 480 heures ou 435 jours ou travail.
Si vous gagnez 100 000 $, vous gagnez 50 $ de l'heure. 87 000 $ = 1 740 heures ou 217,5 jours ou travail.
C'est plus facile de voir une année de travail supplémentaire, non ?
Si vous avez besoin de plus d'un visuel… 87 000 $, c'est aussi quatre Toyota Corolla 2020 :

Ou vous pouvez emmener 86 personnes sur cette croisière en Alaska (ou la faire 86 fois !) :
Les opportunités de dépenser 87 000 $ sont infinies!
Comment la composition s'applique à la vie
Si vous ne connaissiez pas les mathématiques avant l'équation ennuyeuse, comprendre comment les nombres fonctionnent ne vous convient probablement pas. Je ne te blâme pas. Les chiffres sont antiseptiques.
Mais donnez-moi un instant et j'expliquerai comment la composition s'applique à vie.
Pensez à vos relations les plus proches et les plus fortes – quand les avez-vous rencontrés? Combien de temps, au total, avez-vous passé avec eux ?
Si vous êtes comme la plupart des gens, les personnes dont vous êtes les plus proches sont aussi celles avec qui vous avez passé le plus de temps. Vous les avez peut-être rencontrés il y a longtemps ou plus récemment, mais le thème est le temps que vous avez passé ensemble. L'intensité de ce temps compte aussi.
Tes parents. Vos amis d'enfance. Vos amis de collège.
Considérez ceci - votre relation a composé sur une longue période de temps. Les petites interactions, comme un petit pourcentage d'intérêt, s'accumulent sur de nombreuses années.
Interrogé, Robert Waldinger, le directeur du Étude de Harvard sur le développement des adultes où ils ont suivi la vie de 724 hommes tout au long de leur vie, ont déclaré que l'un des facteurs les plus importants pour déterminer le bonheur était la proximité de vos relations. La conférence TED de Waldinger est à seulement 13 minutes et l'un de mes favoris.
La raison pour laquelle vos relations se renforcent avec le temps est que vous accumulez des souvenirs ensemble. Vous construisez la confiance sur plusieurs instances où vous devez vous faire confiance. Vous étiez coincé dans la circulation sur le chemin du retour et ils sont venus chercher vos enfants à l'arrêt de bus. Vous avez oublié de fermer votre porte de garage, alors ils se sont arrêtés pour lui demander le bouton. Un érable massif est tombé et vous avez aidé à le dégager.
Au fil du temps, ces moments se construisent les uns sur les autres, un peu comme des intérêts composés. Au final, votre relation est plus forte. C'est composé.
Certains de mes amis les plus proches sont ceux que j'ai rencontrés via Internet. Nous avons travaillé ensemble sur des projets, réfléchi lors d'appels téléphoniques et passé du temps ensemble en personne à le découper autour de boissons pour adultes. Le temps cumulé que j'ai passé avec eux en personne pourrait être inférieur à une semaine. Mais avec Internet et la messagerie, il est facile de communiquer et d'interagir avec quelqu'un pendant une longue période sans être réellement en présence l'un de l'autre. Ces microtransactions établissent des relations malgré le fait que le contact soit assez minime.
Je vous laisse avec un dernier exemple de quelqu'un que j'ai rencontré il y a des années avant qu'il ne devienne le gourou des habitudes car il explique exactement ce principe mais dans un domaine différent. L'article de James Clear sur Amélioration continue explique comment 1% d'amélioration semble si petit mais avec le temps peut être énorme (il n'a pas toujours écrit sur les habitudes mais il a toujours été assez solide avec les mots).
Ce graphique concerne l'amélioration continue, mais il s'agit également d'intérêts composés :

Alors, tout au long de votre journée, pensez aux intérêts composés et à la façon dont ils imprègnent une grande partie de nos vies, pas seulement notre argent.